pfermat's last avatar

three, four, two, one

我不知道为什么这里3和4是倒过来的，虽然有些运算确实需要调整顺序，不过可能有深层次的原因。

The path of love is never smooth

path有路径的意思

smooth是光滑，一般来说指可微性。比如我们说这条曲线是光滑的，就是说这条曲线处处可微；这条曲线是分段光滑的，指曲线的每个分段是可微的，但是在段与段的交接点上可能是不可微的。（不可微最简单的例子：y=|x|，在x=0这点不可微）

But mine's continuous for you

continuous：连续性。简单来说，可以指直观上的连续，没有间断，没有跳跃，具体定义则是，若f在x点连续，则f在x的极限等于f(x)。

You're the upper bound in the chain of my heart

You're my Axiom of Choice, you know it's true

upper bound：上界。这个没啥好解释的。

chain：链，全序子集。所谓序，可以理解成对集合中的元素进行一种按某种大小定义排列的行为。

Axiom of Choice：选择公理。

简称AC，AC在各个数学分支中有各自的表现形式，这里给出一种：

对任意集c，存在以c为定义域的选择函数g，使得对c的每个非空元素x，g(x)属于x。

提及上述的chain（链），其实用Zorn引理描述更好：

Zorn's Lamma，

在任何一个非空偏序集中，若任意链皆有上界，则此偏序集必存在一极大元素。

在ZFC公理假设下（好像是这样吧=w=），选择公理、Zorn引理与良序公理（任意集皆可良序）等价。

AC 在数学基础中具有很重要的地位，看似是一个很无聊很显然的结论，但是缺少了它之后将会导致许许多多重要的结论改写，而承认AC也会导致如著名的 Banach分球悖论。所以，对于不是专注于研究数学基础的人来说，一般倾向于直接承认选择公理，这也就是歌词中说“you know it's true”的原因。

But lately our relation's not so well-defined

relation：关系。若r是a x b（Descartes积）的子集，则r称为集a到集b的关系，(x,y)属于r可以记为xry。

well- defined：良好的定义。我这个翻译有点废柴，具体来说，由于公理化体系是严格建立在几条已确定公理上的，所以对于这个公理系统本身，以及推出的所有 性质、其他定义，都需要确认他们的定义是有意义的，无矛盾的，所以以上定义的relation也需要时无矛盾的，这个大致就称为“well- defined”。

And I just can't function without you

function：函数。

有了relation，我们就可以定义函数：

若a到b的关系f具有性质：对任意的x属于a，有唯一的y属于b使得(x,y)属于f，则f称为a到b的函数。

关于函数，我们通常写成 f:a --> b，更熟悉的写法则是y=f(x)。

I'll prove my proposition and I'm sure you'll find

OMG终于有一句可以完全不用解释了……

We're a finite simple group of order two

group：群。群是代数里最基础、最重要的概念之一。

所谓群，指一个集合G和一个二元运算x，若满足：

(1)结合性：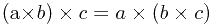

(2)有幺元：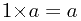

(3)有逆元素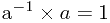：(不知道为啥两个a不一样囧)

以上abc皆为任意G中的元素。

注：群的定义中并没有交换性（axb=bxa），所以上述(2)(3)其实分为左幺元、右幺元和左逆元素、右逆元素，不过在幺元唯一的情况下，应该可以确定左与右是没有影响的。

simple group：单群。

（以下抄袭自百度百科）对于一个有限群G中的任意元素g，若gA与Ag组成的集是相同的，则称G为正规的（normal）。若G的所有子群中，只有单位群（只有幺元的群）与G本身是正规的，则称G为单群。（是不是和素数很像）

finite simple group：有限单群。即群中的元素个数有限。

order：阶。

这里所说的二阶有限单群，是指群中除了幺元外所有元素的阶都是2。

有限单群（在同构的意义下）可以彻底分类，并在上个世纪80年代得到完美解决，这是代数中一个比较NB的结果。

I'm losing my identity

identity：幺元，或者称为单位元。上面已经解释过了。

I'm getting tensor every day

tensor：张量。

代数中的张量定义我实在想不起来了，这里提供一个微分流形中的具体定义。

(p,q)型张量指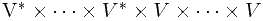(其中V*有p个，V有q个)上的p+q重线性函数。特别地，(1,0)型张量就是V中的元素，而(0,1)型张量是对偶空间V*中的元素即函数。实数是(0,0)型张量。

然后我发现上面那句不用解释的歌词还是需要解释……

“我”是一个Z2群，“你”也是一个Z2，所以将我们做tensor运算后就得到了2阶的有限单群。

And without loss of generality

I will assume that you feel the same way

这句歌词很神，路人听到之后大笑，。解释如下：

without loss of generality：不失一般性。

在讨论某些问题时，并不需要考虑所有的情况，取某些特定的代表就可以搞清楚整个状况，这时候最爱用“不失一般性”这几个字；

assume：假定。举例来说，x是实数，而我们发现讨论这个问题时x的正负性并不重要，因此这么说，“Without loss of generality, assume x > 0.”

综上，这句歌词的含义就是，不失一般性，取“我”为代表，而“你”和“我”其实都是Z2，所以结论是一样的，自然你的feeling和我是一样的。

Since every time I see you, you just quotient out

The faithful image that I map into

这句不想解释了，因为关于商映射（quotient map）还有faithful image我知道的不是很清楚，怕解释错了。

But when we're one-to-one

You'll see what I'm about

one-to-one：一一的。这个一般指一一对应关系，就是从a出发找到唯一一个b，而从b出发也能找到唯一的a。

'Cause we're a finite group of order two

 

Our equivalence was stalbe

equivalence：等价关系。

若集A上的二元关系R满足以下三条性质，则称R为等价关系：

(1)自反性：xRx

(2)对称性：xRy ==> yRx

(3)传递性：xRy, yRz ==> xRz

其中xyz皆为A中任意元素。

A principal love bundle sitting deep inside

But when you drove a wedge between our two-forms

关于principal bundle（主丛）、wedge（外积）、tow-forms（2-形式）都涉及到微分流形中的一些概念，解释起来要花很大的篇幅，我就不多说了。

Now everything is so complexified

（这是题外话）我没记错的话，外积一次后变成2-形式，不过这里的complexified有没有什么复化的含义我就不知道了。

When we first met, we simply connected

simply connected：单连通。

所谓单连通空间，指所有闭曲线皆能连续地收缩到一点。由此可知，球面是单连通的，而环面不是。

My heart was open, but too dense

open：开集。开集在不同的分支各有具体的定义，我就不解释了，有兴趣的可以去翻一下wiki。

dense：稠密。所谓稠密性，指任意a不等于b，则在a与b之间必存在一个c。有理数集是稠密的，自然数集则不是。

Our system was already directed

To have a finite limit, in some sense

directed：定向的。这个不太明白，只知道拓扑中有可定向/不可定向的概念，但是在这里是何含义无法理解。

注：根据参考文献中的说法，这里和Klein群以及四元数有关，是不是因为把两个Z2叉起来的关系。另外作为实数的不断扩展，从复数到四元数，不断地也不可避免地丢失了一些实数有的性质，例如复数不能比较大小。

I'm living in the kernel of a rank-one map

kernel：核。f是一个映射，所有的f(x)=0中的x组成的集合就是f的kernel。

rank：秩。

From my domain, its image look so blue

domain：定义域。

image：像。f(a) = b，把b称作a在映射f下的像。

'Cause all I see are zeroes, it's a cruel trap

kernel里的点都被映射成了0，自然是all zeroes了。

But we're finite simple group of order two

 

I'm not the smoothest operator in my class

operator：算子。

class：类。这个又有点泛函里的说法了，不解释。

But we're a mirror pair, me and you

根据参考文献的解释，因为你和我都是相同的Z2，所以相当于一种镜像。

So let's apply forgetful functors to the past

参考文献中没有解释，我觉得forgetful functors应该是遗忘函子的意思，不过这个涉及到代数拓扑中的内容，我需要去请教一下同学。

And be a finite simple group, a finite simple group

Let's be a finite simple group of order two

 

Why not three?

为什么不是三阶的？

I've proved my proposition now, as you can see

So let's both be associative and free

associative：结合性。之前解释过了。

free：自由。一个群G所谓是自由的，指如果存在G的子集S使得G的任何元素都能唯一地表成由S中元素及其逆元组成之乘积；此时也称G为集合S上的自由群，其群结构决定于集合S，记为F(S)，S称作一组基底。

And by corollary, this shows you and I to be

Purely inseparable. QED

purely inseparable：纯不可分。这又涉及到群的概念，我仍旧需要去请教一下同学……

QED：证毕，也可以写成一个小方块。

 

以下抄袭自参考文献：

歌 词用函数关系类比了两人关系，用从Z_2生成二阶有限单群的过程来象征两人的结合。一开始“我”和“她”是两个集合（Z_2），如果想在两个集合间建立 起一个函数关系，必须要定义出一个relation，但一开始这个relation是不完备的。之后作者又非常巧妙地利用了群的第一同态定理，通过商映射 把真实和虚幻联系了起来，解释两个人在感情发展过程中有过的误会与不愉快……当然最后还有那些很重要的那个二阶有限单群的性质，作者太有才了……

 

[参考文献]：http://www.oiegg.com/viewthread.php?action=printable&tid=711121